已知三角形边长,计算三角形的角度过程如下: 1、设三角形中角A所对应的边长是a,角B所对应的边长是b,角C所对应的边长是c。 再利用公式: ①CosA= (c^2b^2a^2)/2bc ②CosB= (a^2c^2b^2)/2ac ③CosC= (a^2b^2c^2)/2ab 算出每一个角的余弦值,利用计算器上的反
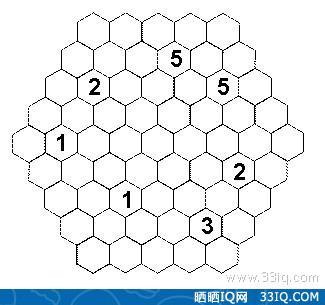
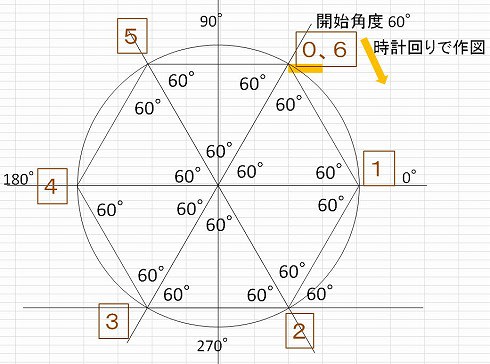
6角形 角度- 三角形の辺の長さなどから角度(角の大きさ)を求める方法です。 次の2パターンに分けて説明します。 パターン1:3辺の長さから角度を求める方法 パターン2:2辺の長さと1つの角度から残りの角の大きさを求める方法角度和弧度及三角函数 生活中一般旋转多少角度(rotation),是以"度"为单位;而在三角函数里的角度要以"弧度"为单位。 "度"的定义是: 两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。 当这段弧长正好等于圆周长的360分之一时,两
6角形 角度のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  | |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「6角形 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |
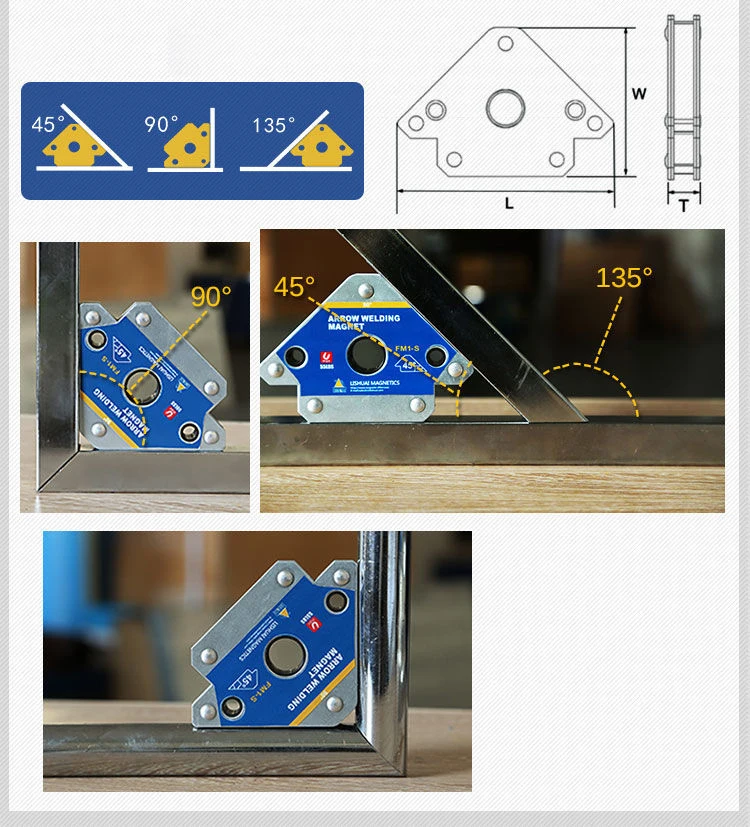
从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少?6角形及12角形的應用有何差異 兩者差異: 1推出時間: 六角形為傳統形狀,而十二角則是較晚開發出之產品,確較為普遍。 2功能: 特色在越多角則均分角度越小,要套入螺絲所須旋轉之角度也越少,不用轉動過大的角度。(如下圖) 3外形尺寸:





0 件のコメント:
コメントを投稿